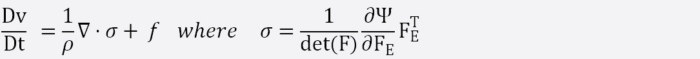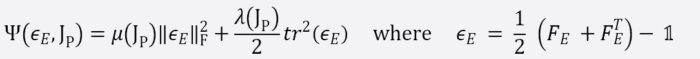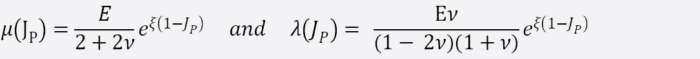Snow Solver in PreonLab

Snow creates deeply physical experiences that can remain vivid memories: Seeing snow for the first time, a snow crystal melting on your tongue, a snowball fight, the different activities summarized as winter sports. However, snow also affects human activity and can, quite literally, get in the way. Snowplows clear roads, highways, airfields and railroads. Snow drifts may destabilize structures due to uneven loading. Avalanches and blizzards are natural hazards that can endanger living beings.
PreonLab solves many automotive problems. When it comes to snow, one is foremost interested to prevent soiling of critical components. The number of tasks is vast. Some that PreonLab has already solved are: Placing cameras for self-driving cars, snow entering the engine air intake which can cause a power drop or localizing corrosion hot-spots in the wheelhouse. Audi and Great Wall Motor are just some examples demonstrating the snow solver capabilities to simulate and capture phenomenas measured in real world test setups at different vehicle speeds. Out of the many sensors PreonLab provides, the addition of the height sensor has been key for the engineers to assess soiling.
So how does PreonLab achieve this? Let’s take a step back and look what we are up against.