PreonLab
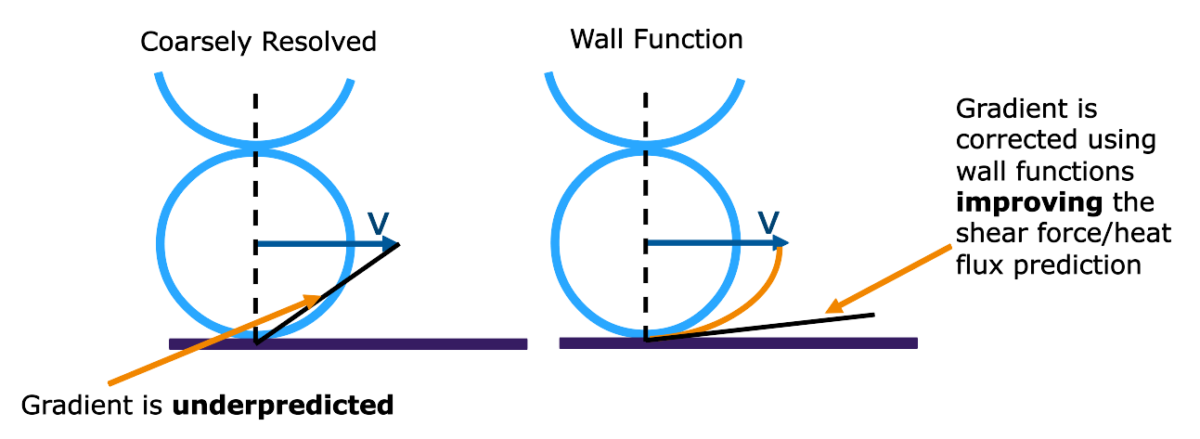
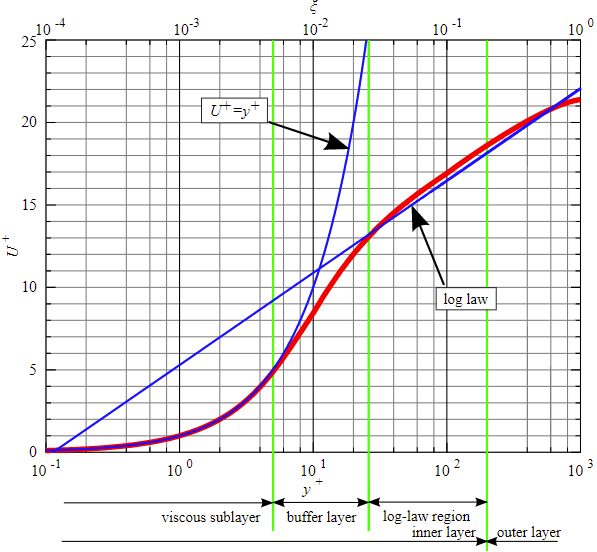
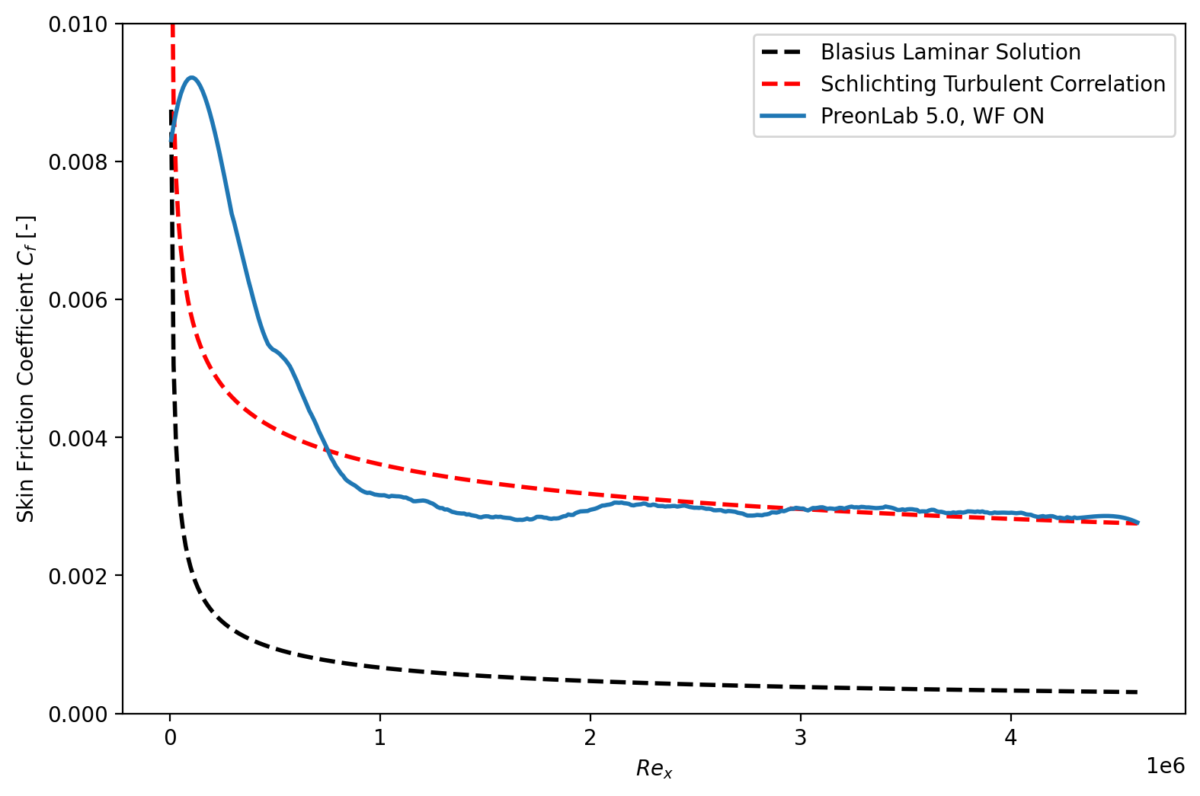
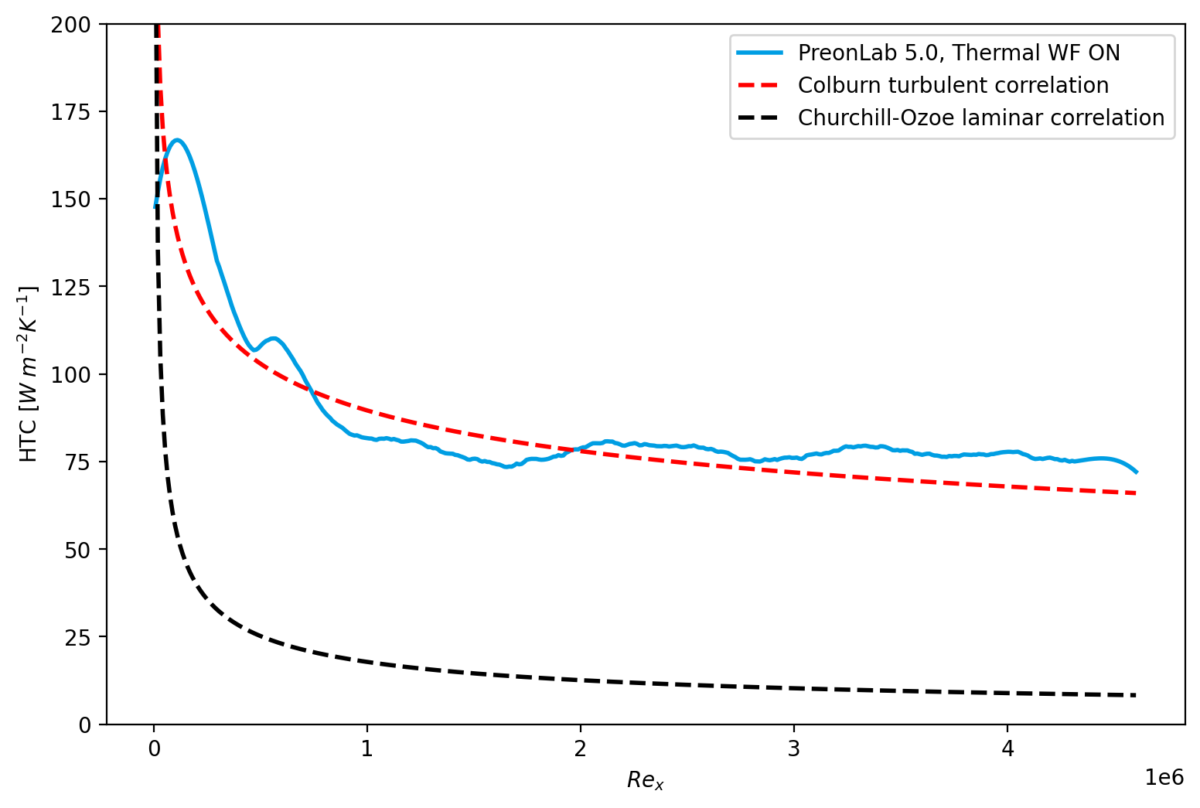
Wall Functions
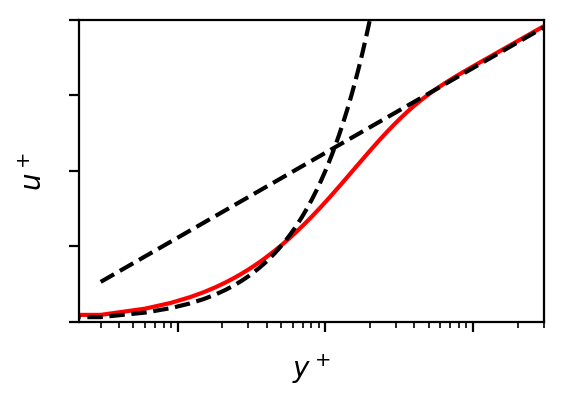
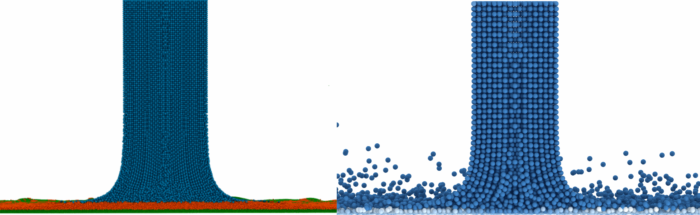
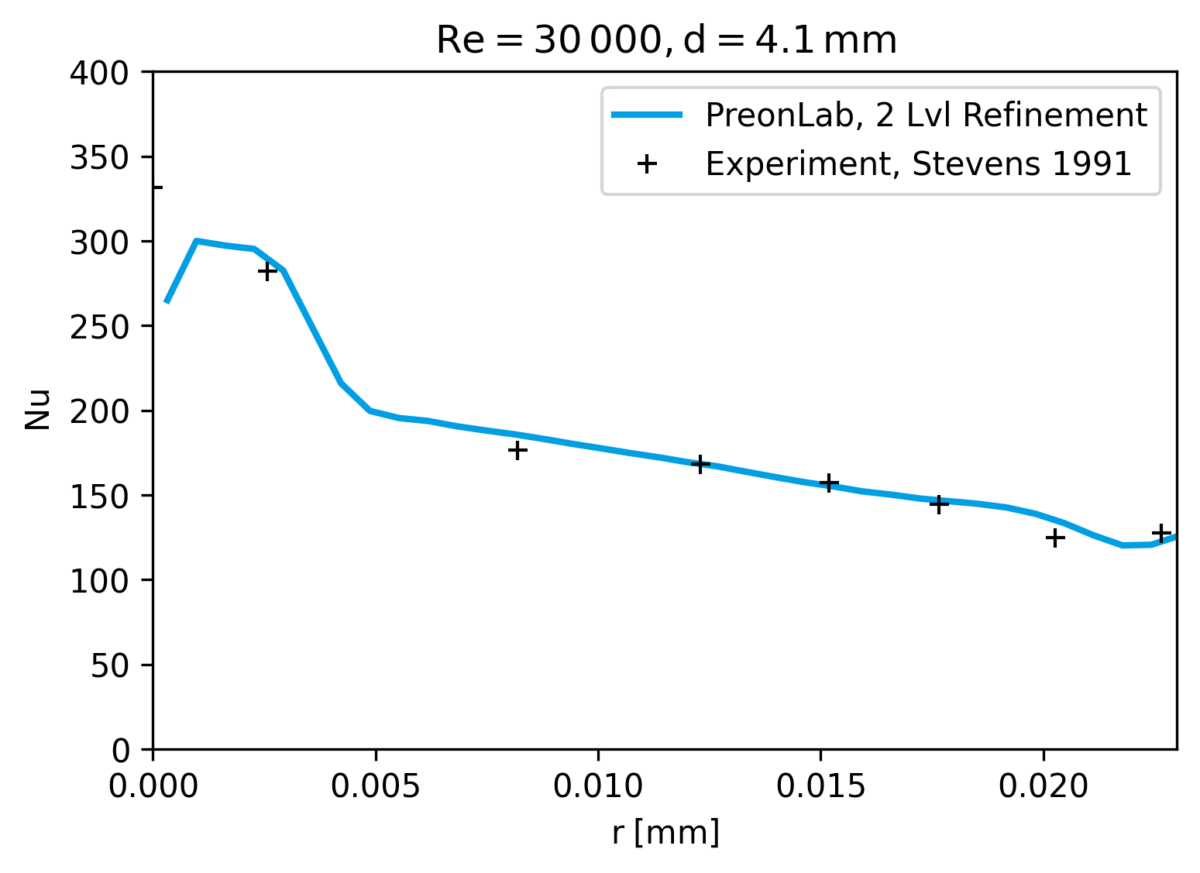
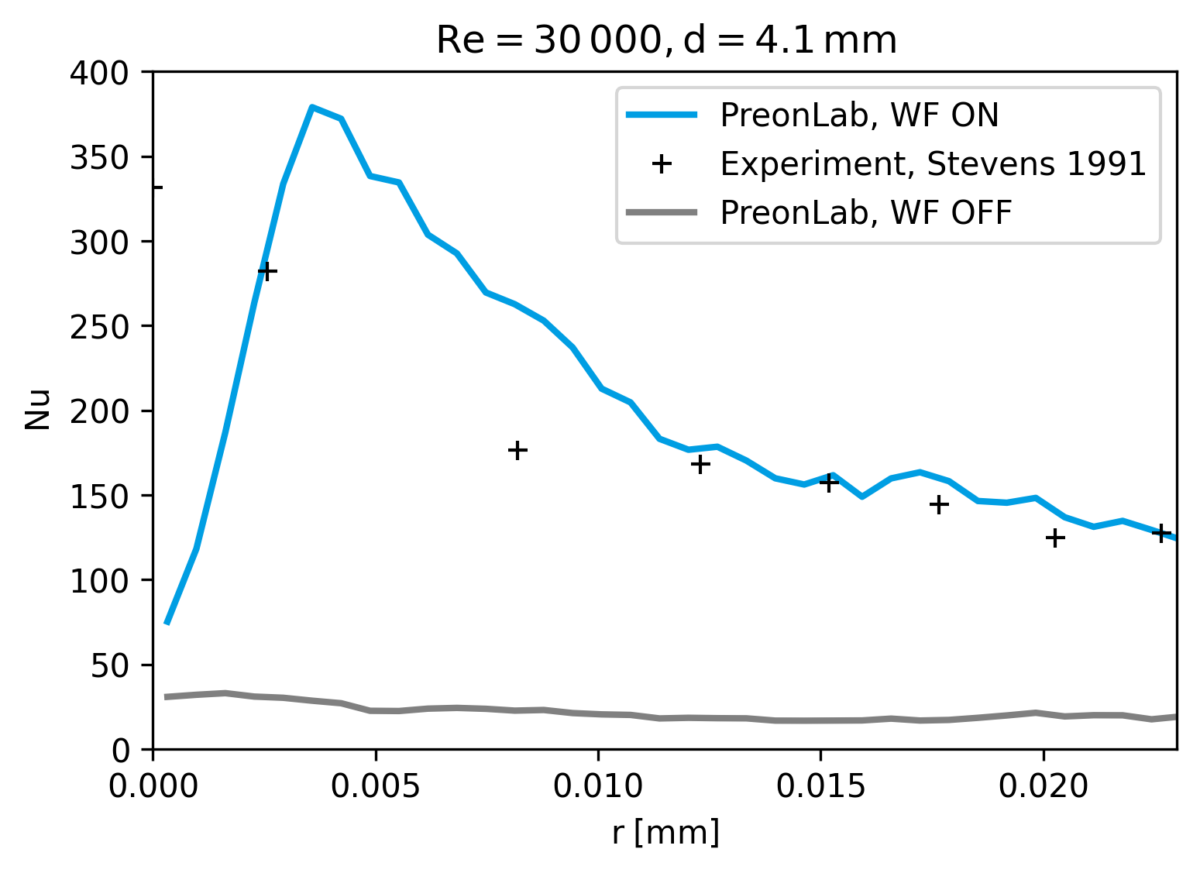
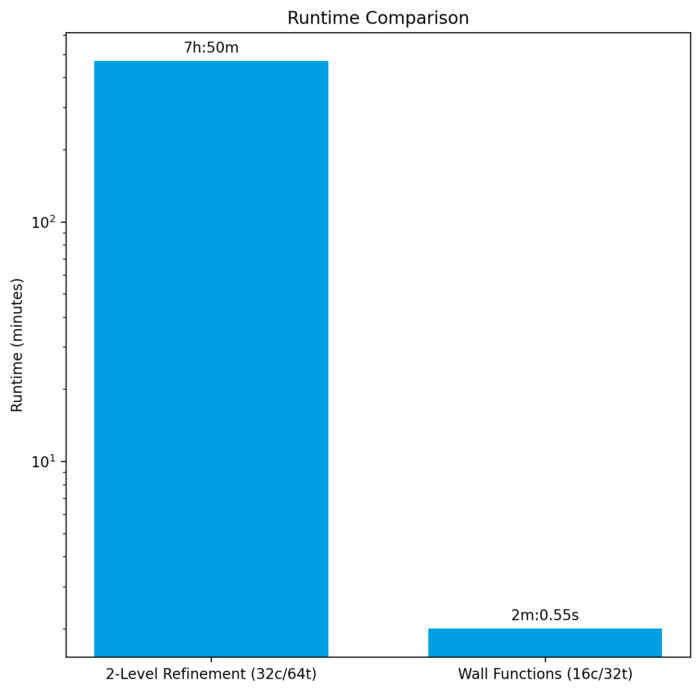
For coarsely-resolved simulations, especially those for applications that require numerous quick design iterations to asses the plausibility of a design, a simulation that both runs quickly and delivers results in the correct ballpark is needed. The coarse resolution allows for fast computation, but such simulations tend to suffer from gradient underprediction at the walls. This happens in particular for flow regimes which may be considered as turbulent, where the steep gradients at the wall mean that a very fine resolution is required to correctly reproduce them. With the effect of wall-bounded phenomena (e.g. wall shear stress, wall heat flux) being a key result for studies that such simulations are used for, it is clear that there is potential for improvement here.