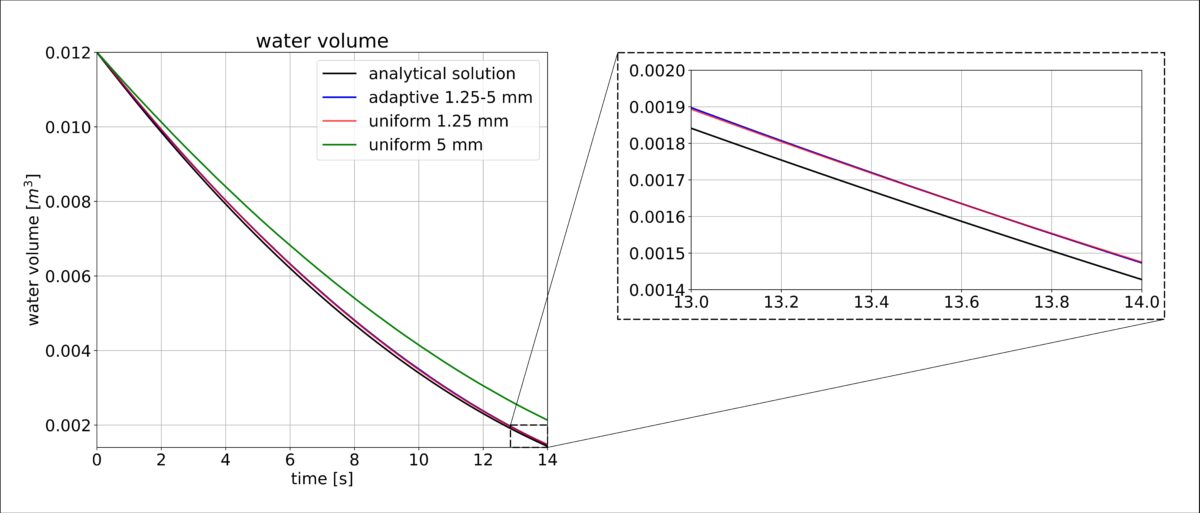
Figure 1 shows a simple setup in which a box with a hole at the bottom is filled with fluid. According to Torricelli’s law, the speed of the outflow is related to the height of the fluid above. This is a great benchmark for CFD solvers because it is possible to compute the speed of the outflow analytically. We will compare three setups: Two will use a uniform particle size with 5 mm and 1.25 mm respectively. Another setup will use three particle sizes with diameters ranging from 1.25 mm to 5 mm. To this end, a refinement domain is placed around the outflow, so that a particle size of 1.25 mm is used there. PreonLab automatically refines the particle layer between the 1.25 mm and 5 mm particles to 2.5 mm.
Figure 1 shows the high-resolution uniform simulation and the adaptive simulation side by side for a visual comparison. Figure 2 shows how the volume inside the box changes over time. The adaptive simulation produces almost the same result as the simulation with a uniform particle diameter of 1.25 mm. Both are much closer to the analytical solution than to the coarse simulation with 5 mm particle diameter.
The adaptive simulation ran more than 12 times faster than the uniform simulation with 1.25 mm particle size. This is a very promising result and shows that the adaptive solver can speed up some applications by an order of magnitude. This speed-up will vary from case to case, but we expect that all applications which simulate large fluid volumes (such as water wading) can be accelerated significantly.
Reduced computation time is the most obvious advantage of the adaptive simulation, but it is not the only one. In the Torricelli scene, the average number of particles and the disk space consumption decreases by a factor of 22. Fewer particles mean that transferring data from a cluster is much faster, viewing the results on a laptop is smoother and archiving the results requires less hard drives.