The next level
Adaptive Particle-based Simulation in PreonLab
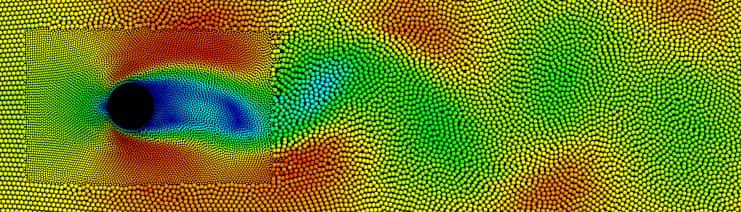
Particle-based fluid simulation methods such as implicit SPH have many advantages over Eulerian grid-based methods. You can read all about it here.
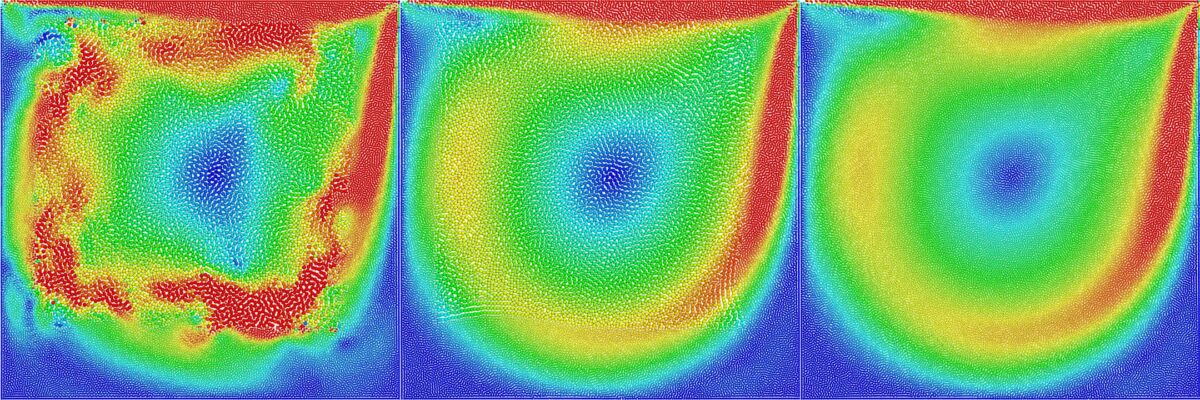
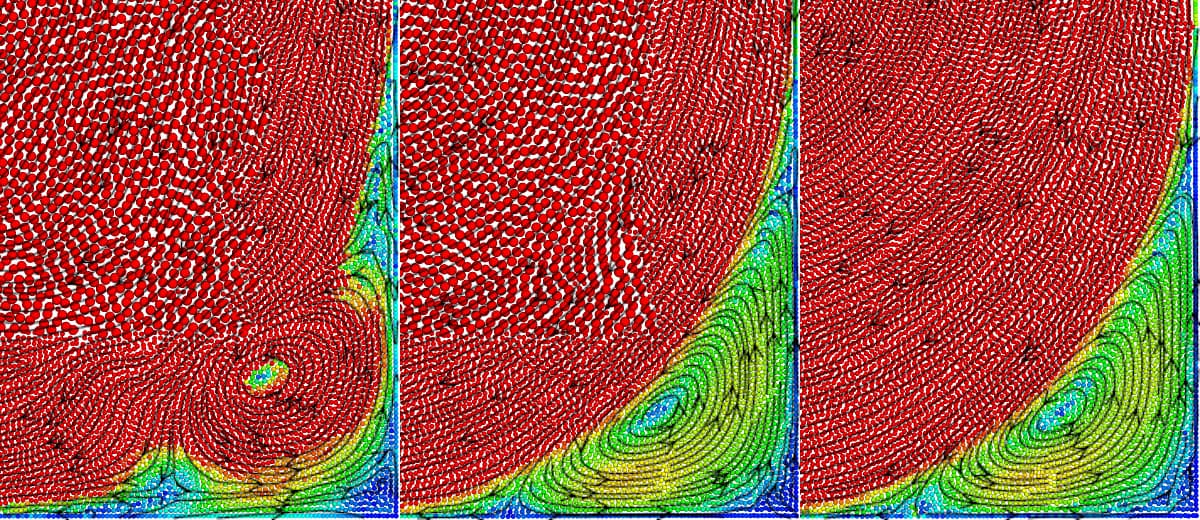
One advantage that Eulerian approaches still enjoy over most particle-based solvers is the ability to model fluid adaptively. By using finer cells in regions of interest and coarser cells in others, an adaptive mesh can reduce computational effort by several orders of magnitude. If multiple levels of detail are so clearly beneficial, why are they still relatively rare for most particle-based solvers?